La rejilla óptica tiene su base de sustentación en un principio físico demostrado y desarrollado por Young hacia la segunda mitad del Siglo XVII, llamado “Interferencia de Rayos Lumínicos”, y más precisamente del fenómeno de difracción derivado de aquel (del cual toma las bases fundamentales para producir sus efectos). En este trabajo trataremos de acercarnos a la interpretación de estos fenómenos para aproximarnos así a la comprensión de la rejilla óptica y sus aplicaciones.

Hasta la primera mitad del siglo XVII se creía que la luz consistía en la emisión, por parte de focos luminosos específicos (por ej. El sol), de pequeños corpúsculos. Estos últimos, por ser extremadamente tenues y por viajar a gran velocidad, no eran atraídos por la fuerza gravitatoria por cuanto su propagación se realizaba en línea recta hasta llegar a la retina, excitando así el sentido de la vista. La teoría corpuscular de la luz (expuesta por Newton) si bien resultaba apropiada para explicar la mayoría de los fenómenos hasta entonces conocidos (reflexión, refracción, etc.) no pudo ser aplicada al fenómeno de doble refracción recientemente descubierto.

Hacia mediados del año 1670, Christian Huygens formula una nueva teoría considerando a la luz como un movimiento ondulatorio de características vibratorias (es decir mecánicas) que atraviesa un medio elástico y continuo llamado éter que se extiende por todo el espacio y penetra todos los cuerpos. El rayo luminoso consiste, según los postulados de esta teoría, en la propagación de ondas lumínicas a través del éter.

Con la progresiva aceptación de esta formulación pudo demostrarse que el fenómeno de difracción (flexión de las ondas en los bordes de los objetos) que no es sino una parte del fenómeno de interferencia cuya comprobación facilitará la explicación del comportamiento de la rejilla óptica.

Hacia principios del año 1827, Thomas Young logra demostrar que en condiciones especiales, los haces luminosos, considerados como la propagación de ondas de muy pequeña longitud, pueden anularse o reforzarse entre sí, produciendo alternativas bandas de luz u oscuridad perfectamente identificables, lo que constituyó una prueba irrefutable de la naturaleza ondulatoria de la luz.

Cuando dos o más ondas se cruzan en un punto determinado se dice que interfieren en él produciendo zonas de luz cuando llegan en fase o, contrariamente, zonas de oscuridad si llegan en oposición de fase al mismo.

FASE: se denomina así a 2 puntos que se encuentran en el mismo estado perturbatorio.

OPOSICIÓN DE FASE: se le da este nombre a 2 puntos que se encuentran en contrario estado perturbatorio.

Para producir fenómenos de interferencia se necesitan trenes de onda coherentes, esto es, ondas cuyos puntos abandonen siempre en fase sus respectivos puntos de partida (sería sumamente difícil de conseguir con manantiales separados). Es por ello que, para la observación del mencionado fenómeno, se suele utilizar una única fuente de luz que será productora de ondas coherentes tal como lo demuestra la experiencia de Young, que a continuación detallaremos.

Como dijimos anteriormente, se utiliza una sola fuente de luz monocromática de la cual parten infinidad de ondas lumínicas hacia todas direcciones. Parte de estas ondas inciden sobre una pantalla en la cual se practicó una estrecha ranura (S1).

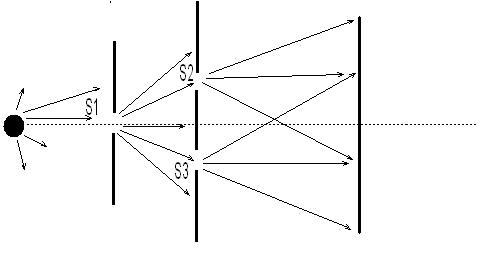
La luz proveniente de esta ranura incide ahora sobre una segunda pantalla con dos ranuras similares y paralelas a S1 y equidistantes entre sí (S2 y S3).

Si se coloca una tercer pantalla a continuación de las anteriores se observa una sucesión de franjas brillantes y oscuras alternativamente paralelas a las rendijas.

Si se cubre una de las hendiduras S2 o S3, las franjas oscuras desaparecen y sólo se ve una franja ancha de luz.

La teoría corpuscular no pudo explicar el hecho de que en un punto de la pantalla, luminoso cuando está abierta la ranura, se transforme en un punto oscuro cuando están abiertas las  dos. Se ha producido un fenómeno de interferencia de ondas lumínicas que trataremos de exponer brevemente en este trabajo.

En la figura 2 vemos que de S1 parte un tren de ondas que alcanza en un mismo momento las ranuras de S2 y S3. Desde allí se producen ondas secundarias que abandonan en fase S2 y S3 respectivamente, actuando ambas como manantiales coherentes.

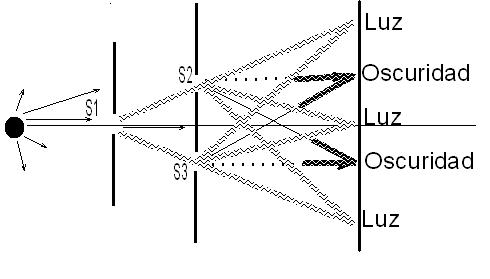
En la parte central de la pantalla (3) aparece una franja de luz. Esto es posible ya que las ondas provenientes de las 2 ranuras siguen caminos de igual longitud de onda sumándose en fase entre sí.

Pasa lo mismo con los puntos 1 y 5 donde, si bien el recorrido de ambas ondas es distinto (Por ej. En 1 la onda proveniente de S2 recorre una distancia mayor que la que parte de S3), la diferencia entre los dos equivale a la longitud de onda de la luz incidente llegando en fase a los puntos mencionados.

En los puntos 2 y 4, en cambio, la diferencia de recorrido de las dos ondas es de ½ longitud de onda, llegando a la pantalla en distintos estados perturbatorios o sea, en oposición de fase. De esta manera, ambos trenes de onda se anulan entre sí, provocando las rayas oscuras observadas en la pantalla 3.

Se han producido interferencias constructivas en los puntos 1, 3 y 5 ya que la diferencia de trayectos equivale, como dijimos anteriormente, a la longitud de onda de la luz empleada. En los puntos 2 y 4 las interferencias son destructivas ya que los trayectos recorridos por ambos trenes de onda corresponden a un número impar de semi longitudes de onda.

Reemplazando el manantial monocromático por uno policromático, en la pantalla aparecerán franjas coloreadas en vez de las brillantes y oscuras. Esto se debe a que la ausencia de un color, provocada por la interferencia en oposición de fase de dos ondas, no produce oscuridad sino la aparición de su complementario.

Tratándose de fuentes policromáticas (Ej. : luz blanca que contiene a todos los colores). Cada uno de ellos producirá su propia figura de interferencia puesto que a cada color corresponde una longitud de onda determinada que, al chocar con la pantalla, se anula o refuerza según llegue en fase o no con su similar (proveniente de otra rendija). Podemos observar este fenómeno en una capa de aceite sobre el pavimento, donde una parte de la luz que incide sobre ella es reflejada en la primera cara y otra parte en la segunda cara de dicha capa, llegando a nuestra retina con recorridos diferentes anulándose o reforzándose mutuamente.

Según los principios de la Óptica Geométrica, si colocamos un objeto opaco, entre una fuente luminosa y una pantalla, los bordes del mismo arrojarán una sombra netamente definida observándose que no llega luz a la pantalla en los puntos situados sobre esa sombra geométrica por los bordes del objeto sobre, por ejemplo, una placa fotográfica observaremos que la sombra  aparece bordeada por bandas oscuras y brillantes alternativas. Esto se debe a que una pequeña cantidad de luz ha penetrado en la sombra geométrica (dando vuelta la borde del objeto) produciendo bandas brillantes en donde, teóricamente, debería aparecer oscuridad.

Este fenómeno se conoce con el nombre de difracción definida como la flexión de las ondas luminosas alrededor de un obstáculo. La difracción de la luz es, en rigor, un fenómeno de interferencia.

Según el principio de Huygens, cada punto de un frente de onda debe considerarse como el origen de una onda secundaria que se propaga en todas direcciones. Los fenómenos de difracción solamente son observables si parte del frente de las ondas es eliminado por algún obstáculo (Ej.: rendija).

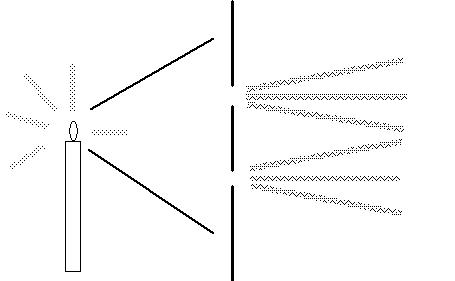
Podemos calcular la luz que llega a un punto P de la pantalla S2 aplicando el principio de superposición a todas las ondas secundarias que llegan a él. Cada onda secundaria recorrerá una distancia diferente a las demás para llegar  P y el ángulo que forme con la luz incidente también será distinto, motivo por el cual variarán las amplitudes y fases de las ondas secundarias que lleguen al punto.

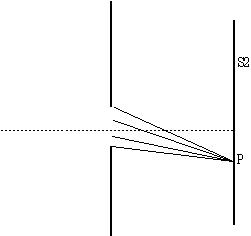
Si la pantalla S2 está los suficientemente alejada o la rendija es bien estrecha, lograremos que las ondas secundarias que parten de A-A’ puedan considerarse paralelas al llegar a un punto determinado de la pantalla S2.

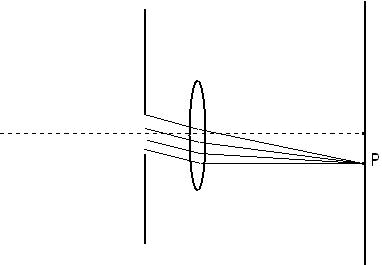
Esta es la llamada Difracción de Fraunhofer que se presenta si colocamos una lente muy próxima a la hendidura pues la misma concentra en su punto focal imagen las ondas secundarias que parten de aquella y se propagan en una dirección determinada.

Cuando la pantalla está muy próxima a la rendija o ésta es relativamente ancha se trata de Difracción de Fresnel.

Consideramos dos rayos que parten de la hendidura A-A’. Uno de ellos parte del borde superior y el otro de la línea media de la rendija y ambos son paralelos tal que forman un ángulo con respecto a la luz que les dio origen.

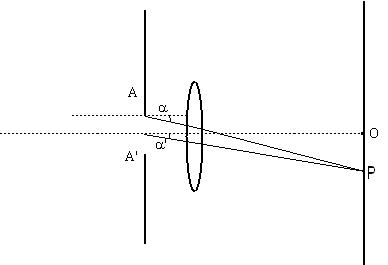
Como se explicó anteriormente, al ser ambas ondas secundarias (provenientes del mismo manantial monocromático) parten de la rendija en concordancia de fase. Sin embargo, la onda superior recorrerá un camino mayor para llegar a la pantalla en el punto P.

Las ondas secundarias que lleguen al punto O de la pantalla no formarán ningún ángulo con respecto a la luz incidente alcanzando en concordancia de fase dicho punto. Se produce así una suma de amplitudes que da por resultado la aparición de una figura de difracción central brillante (máximo).

Considerando puntos sobre la pantalla, cada vez más separados del centro, el 6aacute;ngulo aumenta y con él la diferencia de recorrido. En el momento en que esta diferencia equivale a media longitud de onda, ambas ondas llegarán en oposición de fase a la pantalla anulándose mutuamente y produciendo, por lo tanto, las franjas oscuras de la figura de difracción (mínimo).

En otro punto de la pantalla, todavía más alejado del anterior, la diferencia de recorrido equivale a un número par de longitudes de onda llegando ambas en fase nuevamente. Se produce, por lo tanto, otra faja brillante (segundo máximo) contigua a la oscura pero de una intensidad mucho menor a la central. La intensidad en esta faja central es aproximadamente veinte veces mayor que en el máximo siguiente y, por ello, la mayor parte de la luz está concentrada en ella.

Otra característica importante de esta franja central es que su ancho es mucho mayor al ancho de las rendijas consideradas individualmente. Esto es fácilmente demostrable por medio de un procedimiento  matemático simple que obviaremos: una rendija, con una anchura igual a 5 longitudes de onda respecto a la longitud de onda de la luz incidente, produce una franja central brillante de 1 cm de ancho con la pantalla colocada a 5 cm de la rendija.

El agujero estenopeico constituye un ejemplo claro de difracción de Fraunhofer pues a través del mismo se producen ondas secundarias que, atravesando el cristalino, convergen en la pantalla constituida por la retina produciéndose sobre la misma el máximo de luminosidad de la figura de difracción.

Cuando hay más de una rendija se produce un fenómeno de difracción combinado con uno de interferencia. Cada rendija produce su propia figura de difracción en donde la intensidad de los máximos está relacionada con el ancho de hendidura; los haces de esta figura interfieren entre sí para producir la figura central.

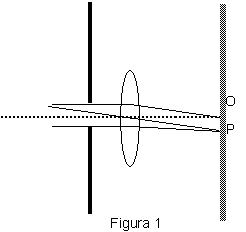
Tomemos dos rendijas detrás de las cuales se ha colocado una lente convergente. La pantalla, en ambos casos, estará colocada en el plano focal imagen de dicha lente.

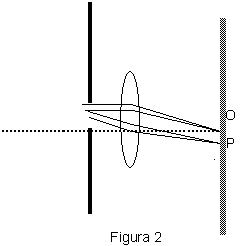
En la figura 1, el eje de la rendija coincide con el eje de la lente. En la figura 2, el eje de la rendija estará por encima del eje de la lente.

Figura 1: tomamos dos haces refractados, uno de ellos produce el primer máximo central (O) y el otro en primer mínimo (P). Vemos que el m6aacute;ximo central se encuentra sobre el eje de la lente.

Figura 2: la figura de difracción coincide con el eje de la lente (como la figura 1) y no con el eje de la rendija. Esto tiene su explicación: todo rayo paralelo al eje de la lente forma su imagen en el foco imagen de ella.

Podemos deducir que cualquier rendija aislada producirá figuras de difracción de igual intensidad y situadas en la misma posición sobre la pantalla.

La amplitud de ambas ondas es igual y, por esta razón, la faja central tendrá doble amplitud y su intensidad será cuatro veces mayor que la producida por una sola rendija.

A medida que aumentamos el número de rendijas, en el punto 0 donde la desviación es nula, las amplitudes de las ondas de cada rendija se suman y, en forma proporcional, la intensidad de la figura central es cada vez mayor. Los máximos resultan aún más brillantes y estrechos en tanto los máximos secundarios se hacen casi despreciables.

Si iluminamos la rendija con luz blanca en vez de monocromática, cada color formará su propia imagen de la misma produciéndose una dispersión de la luz en un espectro continuo. En la faja central (punto 0), puesto que la desviación de cada tren de onda proviene de cada color es nula, todos los colores se combinan para dar una imagen de la rendija en el eje de la lente sobre la pantalla (máximo central).

Hemos visto como las figuras de difracción producidas por una o más rendijas son perfectamente observables en una pantalla colocada en forma perpendicular respecto a la luz proveniente de un manantial luminoso (ya sea este monocromático o compuesto por todos los colores del espectro).

Vimos que en la difracción de Fraunhofer, colocando una lente muy próxima a las rendijas, aquella concentra en su plano focal imagen los rayos provenientes del infinito que inciden paralelos entre sí.  La pantalla donde observamos las figuras de difracción está colocada en ese plano de la lente.

Comparemos las figuras 1 y 2:

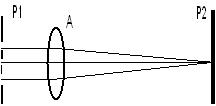
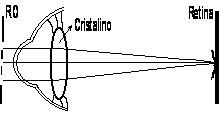
Sustituyendo los elementos de la figura 1 por los de la figura 2, se puede apreciar que la Rejilla Optica, con sus perforaciones, actúa de la misma forma que la pantalla P1, siendo cada hendidura productora de ondas secundarias. Tal cual hemos visto anteriormente, cada tren de estas ondas secundarias partirá de las perforaciones de la rejilla óptica, llegando al cristalino (lente de la figura 1) para luego concentrarse en el plano focal imagen del mismo constituido por la retina que, a modo de pantalla (P2 en la figura 1), recogerá las figuras de difracción anteriormente descriptas.

A lo largo de todo este trabajo tres puntos merecen especial atención:

A.    La figura de difracción central por una rendija tiene 20 veces más luminosidad que la luz que le dio origen.

B.    Cuando se trata de dos o más rendijas, las ondas secundarias provenientes de cada una de ellas suman sus amplitudes en la faja central de la figura de difracción ya que todas llegan a la pantalla en fase por ser su desviación nula con respecto a la luz incidente.

C.    Una rendija da, por ejemplo, 5 longitudes de onda respecto a la longitud de onda de la luz inicial, formando en una pantalla colocada a 5 cm de la misma, una faja central brillante de aproximadamente 1 cm de ancho.

De todo esto podemos inferir que a mayor cantidad de rendijas aparecerá mayor brillo en la figura central de difracción con la consiguiente nitidez y definición de la imagen. Tal efecto es fácilmente comprobable en los casos observados en gabinete y que presentamos a continuación, lo que implica una afinación de la agudeza visual muchas veces sorprendente, llegando en algunos casos a una recuperación superior al 200% de la visión.

Por otra parte (de acuerdo al punto C), al ser mucho más ancha la franja central que la rendija originaria de la misma, podemos suponer que los máximos y mínimos contiguos a esa figura central de difracción quedarían fuera de la zona de excitación de conos y bastones siendo, por lo tanto, imperceptibles sin dificulta la visión.